Filtri analogici: tipi e loro uso

Il seguente articolo “FILTRAGGIO DEI SEGNALI ELETTRICI”. “Filtri analogici: tipi e loro uso” è stato pubblicato sulla rivista mensile “radiokit elettronica” nel mese di novembre 2020.

FILTRAGGIO DEI SEGNALI ELETTRICI

Filtri analogici: tipi e uso

Butterworth, Cebysev, Elittico e a Cristallo, i nomi dei principali filtri analogici usati negli apparati e accessori di stazione di Radioamatore. In quest’articolo cerco di mettere un po’ di ordine accennando alla struttura, al modo di filtrare e l’uso di ciascuno.

Se analizziamo gli schemi a blocchi del singolo ricevitore e trasmettitore, osserviamo che la presenza di filtri è considerevole sia nella catena di amplificazione a radio frequenza sia in bassa frequenza.

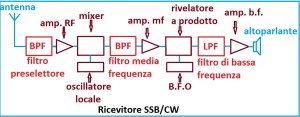
Comincio con i ricevitori, dalla preselezione fra antenna e amplificatore RF con un filtro passa banda per attenuare segnali lontani dalla banda d’interesse e la frequenza immagine, negli stadi a media frequenza per determinare la selettività del sistema ricevente, infine nell’amplificazione a bassa frequenza per sopprimere le frequenze superiori allo spettro della banda udibile. Fig. 1.

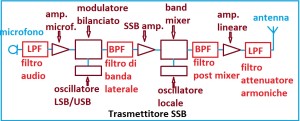
Nei trasmettitori, il segnale microfonico è filtrato per depurarlo da frequenze al di fuori della banda audio, la banda laterale desiderata è selezionata filtrandola dopo il modulatore bilanciato, un altro filtro passabanda seleziona un prodotto di conversione dopo il mixer di banda d’emissione, l’ultimo filtraggio avviene fra l’amplificatore lineare e l’antenna dove un filtro passa basso attenua le frequenze armoniche del segnale trasmesso e adatta l’impedenza d’uscita con l’impedenza della linea di trasmissione. Fig. 2.

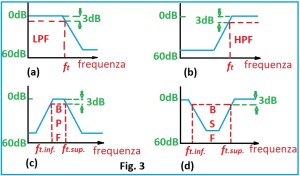
Ci sono quattro tipi di filtro. Filtro passa basso, LPF low pass filter, Fig. 3a, lascia passare i segnali a frequenza inferiore la frequenza di taglio ft e attenua o sopprime quelli a frequenza superiore. Filtro passa alto, HPF high pass filter, Fig.3b, lascia passare i segnali a frequenza superiore la frequenza di taglio e attenua o sopprime i segnali a frequenza inferiore. Filtro passa banda, BPF band pass filter, Fig. 3c, lascia passare i segnali con frequenza all’interno della banda passante, attenua o sopprime quelli con frequenza superiore alla frequenza di taglio superiore e quelli con frequenza inferiore alla frequenza di taglio inferiore. Filtro blocca banda, BSF band stop filter, Fig. 3d, blocca i segnali con frequenza all’interno di un intervallo di frequenze delimitato dalla frequenza di taglio inferiore e superiore, i segnali con frequenza inferiore e superiore alle frequenze di taglio, non sono interessati al filtraggio.

Nella Fig. 3 osserviamo, in maniera stilizzata, la risposta in frequenza, tratto celeste, dei quattro filtri mentre le linee rosse tratteggiate delimitano la banda passante teorica dove i segnali non sono attenuati LPF (Low Pass Filter), HPF (High Pass Filter) e BPF (Band Pass Filter) o la banda in cui sono attenuati BSF (Band Stop Filter). La frequenza di taglio è determinata dal punto in cui la linea orizzontale a -3 dB dalla massima risposta, intercetta il tratto celeste della curva di risposta e proiettato in ascissa dove è rappresentata la frequenza.

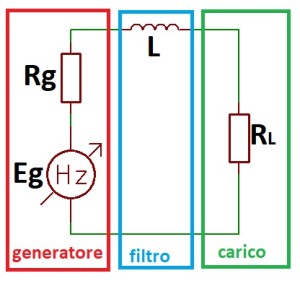
Consideriamo il filtro passa basso LPF elementare di Fig. 4 composto di un solo elemento reattivo, l’induttanza L.

C’è il blocco generatore a frequenza variabile da zero Hz a infinito E_g, con la sua resistenza interna R_g, Il blocco filtro composto dall’induttanza L e il blocco carico composto dalla resistenza R_L.

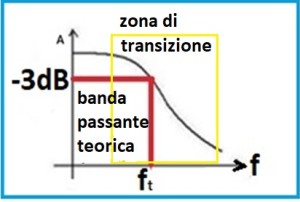
La reattanza induttiva X_L = 2πfL [Ω] prodotta dall’induttanza L, è direttamente proporzionale alla frequenza per questo a zero Hz, corrente continua, non offre nessuna reattanza, tutta la potenza del generatore è trasferita al carico, salvo le perdite. Aumentando la frequenza della corrente generata, l’induttanza L presenta una reattanza induttiva, che equivale a una resistenza, sempre maggiore, di conseguenza, la potenza trasferita al carico diminuisce con l’aumentare della frequenza. La Fig. 5 mostra la curva di risposta del filtro.

Il tratto in rosso è la banda passante teorica, la frequenza di taglio f_t è calcolata a meno 3 dB dal massimo della risposta.

Il filtro appena analizzato è di ordine primo. L’ordine di un filtro s’indica con n, è pari al numero di elementi reattivi presenti nel circuito, capacità e induttanze indipendenti che lo compongono e corrisponde al numero dei poli.

Nel circuito esaminato, osserviamo che il massimo flusso di corrente avviene a frequenza zero Hz, corrente continua, tale frequenza corrisponde al polo del filtro. Nello stesso circuito esiste anche una frequenza, che tende all’infinito, in cui il flusso di corrente tende a zero. Tale frequenza corrisponde allo zero del filtro. I poli e gli zeri si possono disegnare in un diagramma nel cui asse orizzontale vi è la parte reale mentre nell’asse verticale vi è la parte immaginaria, S-plan (9). I poli sono disegnati con una “x” mentre gli zeri sono disegnati con una “o” ai vertici dei vettori che li rappresentano. Ogni elemento reattivo del filtro ha un polo corrispondente alla massima conducibilità, minima impedenza, e uno zero corrispondente alla minima conducibilità, massima impedenza relativamente alla frequenza considerata. Perciò il posizionamento dei poli nell’S-plan per formare i vari tipi di filtro dipende principalmente dall’induttanza e dalla capacità degli elementi reattivi e poi dalla conformazione circuitale.

I poli e gli zeri si trovano operando matematicamente sulla funzione di trasferimento, f.d.t., dei filtri. I valori di “jω” (1) per cui il numeratore tende all’infinito, sono gli zeri. I valori di “ jω” per cui si annulla il denominatore, indicano i poli.

La pendenza della curva nella zona di transizione, area gialla della Fig. 5, fra la massima ampiezza di transito e la massima attenuazione, dipende dall’ordine n del filtro perciò dal numero degli elementi reattivi che lo compongono.

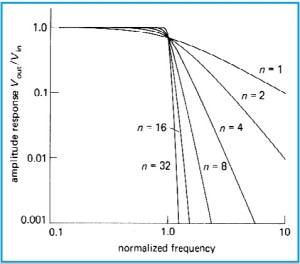
La Fig. 6 (2) mostra la pendenza della zona di transizione per vari valori di n dei filtri, passa basso, LPF.

Maggiore è il numero dei poli e più ripido è il grafico e maggiore è la bontà del filtro. Lo stesso vale per i filtri passa alto HPF, i filtri passa banda BPF e i filtri BSF. La tabella seguente riassume la situazione.

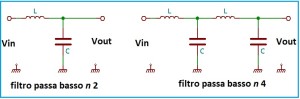
I filtri passa basso, con un adeguato valore di n e frequenza di taglio di 3.000 Hz sono usati nei ricevitori prima dell’amplificatore audio frequenza per ripulire il segnale ricevuto da spurie al di fuori della banda udibile. Lo stesso tipo di filtro è utilizzato all’uscita dell’amplificatore microfonico nei trasmettitori. La Fig. 7 mostra due esempi di filtri passa basso con due e quattro poli. Si nota che quello a quattro poli è costituito da due filtri a due poli collegati in cascata.

I filtri passa basso sono anche usati in uscita nell’ultimo stadio amplificatore a radio frequenza dei trasmettitori per adattare l’impedenza di uscita dello stadio con l’impedenza di entrata della linea di trasmissione.

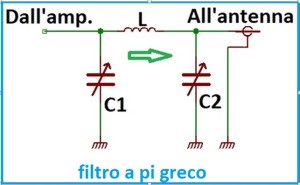
Negli stadi amplificatori a valvole si usa un filtro passa basso a pi greco. La Fig. 8 mostra lo schema.

Con questo filtro a tre poli è garantita un’attenuazione della seconda armonica migliore di 40 dB che per un finale a valvole è sufficiente considerando una curva di transizione poco ripida del filtro n 3. Il condensatore C1 accorda l’uscita dello stadio, assieme all’induttanza L, sulla frequenza del segnale trasmesso. Il condensatore C2 adatta l’impedenza di uscita dell’amplificatore con l’impedenza di entrata della linea di trasmissione, tipicamente cavo coassiale. Il range di accordo varia da circa 30 Ω a circa 75 Ω.

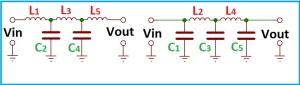
Se il progetto richiede maggiore ripidità nella curva di transizione, bisogna usare un filtro passa basso di tipo Chebyshev con almeno cinque poli che garantisce un’attenuazione maggiore di 80 dB per decade, però presenta un’ondulazione, in inglese ripple, nella banda passante da considerare riguardo alla linearità del segnale in transito. La Fig. 9 mostra due filtri Chebyshev passa basso, il primo con entrata e uscita induttiva il secondo cntata la frequenza.Entrambi hanno valori della componentistica fissi calcolati per realizzare la curva richiesta e impedenza di entrata e uscita fissa, tipicamente 50 Ω.

In internet sono disponibili tabelle per realizzare questi filtri con componenti standard tipo E24 (5). L’uso di tali filtri, in uscita dei trasmettitori a stato solido, comporta collegare in uscita ed entrata dispositivi già adattati, antenne accordate e perfettamente adattate alla linea di trasmissione, oppure l’uso di un accordatore fra filtro e cavo coassiale. Mentre lo stadio amplificatore deve avere l’impedenza di uscita uguale all’impedenza di entrata del filtro. Dal collegamento (6) è possibile scaricare un programma freeware per il calcolo dei filtri analogici L C.

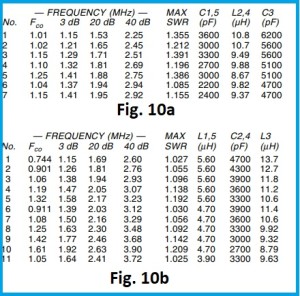
In Fig. 10 (7) un esempio di tali tabelle.

10a entrata e uscita capacitiva, 10b entrata e uscita induttiva. La prima colonna indica il numero dei poli n, nella seconda colonna è riportata la frequenza di taglio in Mhz, nella terza, quarta e quinta colonna sono riportate le attenuazioni rispettivamente a -3dB, -20dB e a -40dB delle frequenze superiori alla frequenza di taglio. La sesta colonna indica l’SWR massimo di tale sistema, mentre le ultime tre colonne sono riportati i valori di L e C riferiti agli schemi di Fig 9. Faccio notare la forte attenuazione delle frequenze superiori alla frequenza di taglio. Considerando la riga n5 di Fig. 10a, con frequenza di taglio 1,25 MHz, alla frequenza di 1,41 MHz, attenua 3dB che è il riferimento della banda passante. A 1,88 Mhz attenua 20 dB e a 2,75MHz attenua 40 dB. Ciò denota una curva di transizione molto ripida tipica di tali filtri.

I moderni amplificatori a MOSFET in configurazione Push-Pull, controfase, hanno la caratteristica che per loro natura attenuano fortemente la seconda armonica, però la terza armonica è presente all’uscita dell’amplificatore con un’attenuazione di appena 20 dB dal massimo della fondamentale. Questa disfunzione costringe i progettisti a usare filtri particolari che oltre ad avere una curva di transizione ripida devono anche presentare nella curva della funzione di trasferimento un noch, zona di particolare attenuazione, in corrispondenza della terza armonica. Questi filtri si chiamano “Ellittici” perché hanno i poli distribuiti nel diagramma complesso S-plan (9) nei quadranti in modo da formare un’elisse.

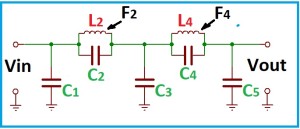
La Fig, 11 raffigura lo schema di filtro ellittico passa basso a cinque poli.

I due circuiti risonanti in parallelo L2/C2 e L4/C4 formano un solo polo ciascuno, anche se gli elementi reattivi sono due per ciascun circuito, essendo in parallelo non sono indipendenti. L2/C2 risuonano nella frequenza F4 e forma un notch in corrispondenza della seconda armonica della fondamentale, L4/C4 risuonano nella frequenza F2 e forma un notch in corrispondenza della terza armonica della fondamentale.

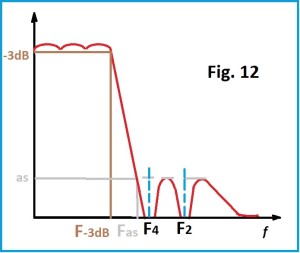
La Fig. 12 mostra il diagramma di trasferimento del filtro ellittico passa basso in cui si vede, il ripple nell’area di attenuazione dove si notano i due notch in corrispondenza di F2 e F4.

La curva di risposta, evidenzia una zona di transizione con curva molto ripida e un ripple pronunciato nella zona di attenuazione con i due notch più evidenti in corrispondenza di F4 per attenuare la seconda armonica e F2 per attenuare la terza armonica. La frequenza F-3dB delimita la banda passante teorica mentre la frequenza F-AS è la frequenza in corrispondenza della massima attenuazione che corrisponde alle cuspidi del ripple della banda attenuata.

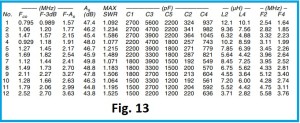
Nella prossima tabella, Fig. 13, tratta da (7), sono forniti i dati per la progettazione del filtro della Fig. 11, riga 5 poli, utilizzando componenti reattivi L e C con valori standard E24.

Riferendoci anche alle Fig. 11 e 12, nella colonna uno c’è il numero dei poli, la colonna due Fco è la frequenza in cui il filtro comincia ad attenuare, la colonna tre F-3 dB è la frequenza di taglio, nella colonna quattro F-As indica la frequenza corrispondente alla massima attenuazione, nella colonna cinque l’attenuazione F-As. Colonna sei il massimo SWR del sistema. Nelle colonne successive il valore delle capacità e delle induttanze per filtri da uno a dodici poli. Per più poli si mettono filtri in cascata. Nella colonna quattordici F2 corrisponde alla frequenza della terza armonica, dove è accordato il circuito risonante parallelo C4/L4, nella colonna quindici F4 corrisponde alla frequenza della seconda armonica, dove è accordato il circuito risonante parallelo C2/L2.

S’intuisce che negli amplificatori a stato solido in configurazione push pull è necessario installare un filtro passa basso in uscita, per ogni banda radioamatoriale in modo da avere un’attenuazione uniforme della terza armonica in tutto lo spettro di funzionamento dell’amplificatore.

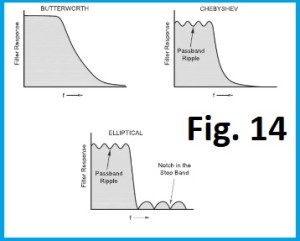
La figura 14 (8) mostra la curva di risposta dei tre filtri considerati finora.

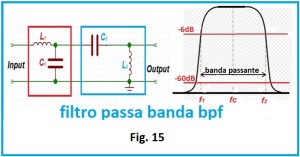
Filtri passa banda. Sono usati nei trasmettitori SSB per selezionare la banda laterale desiderata e nella selezione del segnale dopo il Band Mixer ma la loro funzione è molto importante nei ricevitori, dove sono impiegati all’entrata, Front End, negli Rx di classe alta per eseguire una prima preselezione della banda ricevuta allo scopo di non inviare segnali troppo forti al primo mixer in modo da non sovraccaricarlo e per attenuare la frequenza immagine. Sono usati inoltre come filtri di media frequenza per determinare la banda passante del ricevitore, la selettività. Una delle caratteristiche di tali filtri deve essere la linearità di trasferimento dei segnali. Non ci deve essere intermodulazione fra i segnali che li attraversano in modo da non generare segnali risultanti parassiti e nocivi. Ciò si ottiene utilizzando filtri passa banda tipo Butterworth con banda passante piatta magari aumentando il numero dei poli per migliorare la pendenza dei fianchi per attenuare e sopprimere segnali adiacenti. La Fig. 15 mostra un filtro BPF a quattro poli con impedenza di entrata e uscita di 50 Ω.

Sono un filtro passa basso, riquadro rosso, e un filtro passa alto, riquadro celeste, collegati in cascata. La banda passante è determinata dalla linea rossa a -6 dB, con f1 frequenza di taglio inferiore, f2 frequenza di taglio superiore e fc frequenza centrale nel diagramma di risposta in frequenza del filtro sulla destra della figura. La banda passante a -60 dB dalla cuspide serve capire la ripidità dei fianchi del filtro, più piccola è la differenza della larghezza di banda a -60 dB e a -6 dB e più ripidi sono i fianchi e perciò più alta la qualità del filtro. Nei ricevitori radioamatoriali di classe media è comune trovare filtri di media frequenza a otto poli ma è raro trovare filtri preselettori in entrata.

L’auto costruzione dei filtri di media frequenza è molto impegnativa perché devono essere curate in maniera particolare le loro caratteristiche.

I filtri passa banda a cristallo di quarzo, invece sono meno impegnativi nell’autocostruzione. È sfruttata la proprietà piezoelettrica dei quarzi che vibrano generando una corrente a frequenza che dipende da come sono tagliati, rispetto il loro asse e dallo spessore della lamina del minerale, se sollecitati da una tensione. La caratteristica principale dei cristalli di quarzo è di avere un Q molto alto alla frequenza di risonanza serie con reattanza zero e una risonanza parallelo leggermente più alta in frequenza con reattanza che tende all’infinito. Esaminiamo alcune configurazioni.

I primi filtri a quarzo per media frequenza prevedevano un condensatore variabile opportunamente collegato che doveva cancellare la reattanza parallelo, parassita, del quarzo per avere la massima selettività. Si chiamava condensatore di fase. Il sistema, però, era alquanto instabile e la selettività ottenuta non era abbastanza stretta, massimo 500 Hz ma con fianchi poco ripidi. Lo sviluppo dei filtri a quarzo ci ha portato ai filtri tipo Lattice e ai filtri tipo Ladder.

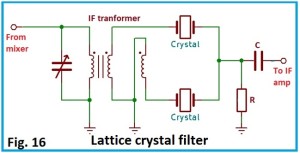
I filtri base, tipo Lattice, a traliccio dalla loro configurazione circuitale, prevedono l’uso di due quarzi con frequenza di risonanza serie molto vicina fra di loro, la differenza di frequenza determina la banda passante del filtro. Più vicine sono le frequenze di risonanza serie dei due quarzi e più stretta è la banda passante. Normalmente sono adatti per il modo SSB con una banda passante di 2,7 kHz. La Fig. 16 mostra un filtro passa banda tipo Lattice con due quarzi.

Il trasformatore di media frequenza è composto di avvolgimento trifilare con primario sintonizzato dal condensatore variabile. I due secondari, cui sono collegati i quarzi, hanno fase opposta, il sistema non ha bisogno di condensatore di fase perciò è molto stabile. Il condensatore C e la resistenza R servono trasferire il segnale all’amplificatore a media frequenza, IF amp, adattando le impedenze. La risposta in frequenza della banda passante ha una leggerissima curvatura al centro ma fianchi molto ripidi.

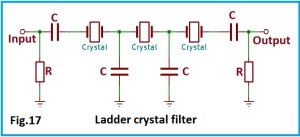
Se si vogliono raggiungere selettività più spiccate con filtri a quarzo, bisogna usare la configurazione circuitale tipo Ladder, a scaletta, in cui usando tre quarzi si possono raggiungere selettività anche inferiore a 500 Hz. In Fig. 17 è raffigurato un filtro Ladder con tre quarzi.

La risonanza serie dei quarzi deve essere molto vicina fra di loro la differenza deve essere meno del 10% della banda passante desiderata. Per una banda passante di 500 Hz la differenza massima deve essere di 50 Hz. I due condensatori verso massa di circa 150 pF ciascuno, servono accoppiare i quarzi fra di loro, mentre le reti R/C, in entrata e uscita hanno R di 150 Ω, C di 200 pF, trasferiscono il segnale e adattano le impedenze.

I filtri a cristallo tipo Lattice e Ladder sono ancora usati perchè affidabili e relativamente economici, non richiedono inuttanze e capacità per determinare la banda passante e mantengono le caratteristiche nel tempo. Sono adatti per radio frequenze mentre per basse frequenze sono più adatti filtri a R/L/C.

In questo articolo ho trattato filtri analogici passivi, devo precisare che, oltre alle caratteristiche di trasferimento citate, tutti i filtri nominati cambiano la fase dei segnali in uscita rispetto l’entrata ma questo aspetto non varia la sostanza dei concetti disquisiti.

Fiorino/i3fdz

Note:

1. Nelle funzioni di trasferimento, nel dominio della frequenza, si usa la notazione S al posto di jω per semplificare i polinomi della frazione. S è un numero complesso che contiene sia ampiezza sia fase, ossia la parte reale e la parte immaginaria.

2. Il diagramma è stato ricavato dal seguente sito:

http://www.diee.unica.it/elettrotecnica/materialeCANNAS/2014-2015/1.IntroduzioneFiltri.pdf

(3) Ottava è l’intervallo di frequenze in cui quella più alta è doppia di quella più bassa.

(4) Decade è l’intervallo di frequenze in cui quella più alta è dieci volte quella più bassa.

(5) https://www.bourns.com/support/technical-articles/standard-values-used-in-capacitors-inductors- and-resistors

(6) http://www.tonnesoftware.com/elsiedownload.html

(7) Le tabelle della figura 10 e 13 sono state ricavate dal volume “The ARRL Hanbook” edizione 1997, nel capitolo “ Filter Design Using Standard Capacitor Values”. Nel capitolo Reference si trovano le tabelle complete.

(8) Tratto dal volume “The ARRL Extra Class License Manual” Ninth edition.

O da questo link: http://www.freqdev.com/guide/analog.html

(9) S-plan, piano complesso a quattro quadranti con asse immaginario verticale H(S), e asse reale orizzontale, per rappresentare il posizionamento, del valore complesso dell’impedenza variabile con la frequenza, dei componenti reattivi e relativi poli e zeri dei sistemi filtranti.