Potenza di picco o potenza media

Il seguente articolo “Potenza di picco o potenza media” è stato pubblicato sulla rivista “Radio kit elettronica” nel mese di novembre 2017.

Potenza di picco o potenza media

Spulciando il “Codice delle Comunicazioni Elettroniche”, Decreto Legislativo 1 agosto 2003, n. 259. Radioamatori, Capo I, Sezione II – Norme tecniche, Art. 15 – Limiti di potenza. Questo articolo dice: “…..omissis… le stazioni del servizio di radioamatore possono operare con le seguenti potenze massime, definite come potenza di picco (p.e.p.) cioè potenza media fornita alla linea di alimentazione dell’antenna durante un ciclo a radiofrequenza, in corrispondenza della massima ampiezza dell’inviluppo di modulazione:
a) classe A, fisso o mobile/portatile 500 W …..omissis…”.
In quest’articolo sembra esserci una contraddizione. Prima si parla di potenza di picco (p.e.p.) e poi di potenza media. La cosa mi ha un po’ confuso. Ho voluto approfondire la faccenda.

Per prima cosa sono andato nel sito della I.T.U. (International Telecomunication Union) per controllare il significato dell’acronimo p.e.p. e la sua definizione ufficiale-
Nella Risoluzione I.T.U. No, 644 della Conferenza Mondiale delle Radiocomunicazioni, Istambul 2000, nella sezione “Definition and terms”, trovo: “PEP” = “Peak Envelope Power”. Con la relativa definizione: “means the average power supplied to the antenna transmission line by a transmitter during one radiofrequency cycle at the crest of the modulation envelope taken under normal operating conditions”. Tradotta letteralmente abbiamo: “significa la potenza media applicata alla linea di trasmissione da un trasmettitore durante un ciclo di radiofrequenza nella cresta dell’inviluppo di modulazione durante condizioni di normali operazioni”.
Dal chiarimento dell’acronimo e dalla sua definizione mi si sono schiarite le idee. La potenza di picco non centra nulla. Ciò che conta per trovare la potenza di emissione legale è calcolare la potenza media di un solo ciclo nella cresta di massima modulazione.
La potenza in corrente continua è: P = V^2/R [W], se invece vogliamo calcolare la potenza in corrente alternata su carico puramente ohmico che produca lo stesso effetto termico di uguale tensione in corrente continua, dobbiamo riferirci alla tensione efficace. La tensione efficace, che d’ora in poi chiamo RMS (Root Mean Square), si trova moltiplicando la tensione di picco di una semionda per 0,707.
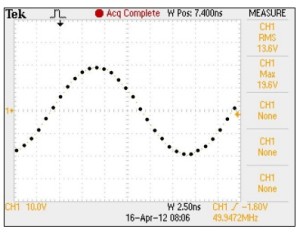
La figura 1,

mostra la schermata di un oscilloscopio con un segnale sinusoidale che è stato campionato. Campionando un segnale con un certo intervallo sommando i valori assoluti campionati e dividendo il totale per il numero di campionamenti del ciclo completo si trova la media del ciclo di segnale sia esso corrente, tensione o potenza qualunque sia la forma.
Se il tempo di campionamento è così breve da essere vicino allo zero, si può utilizzare l’integrazione matematica per ottenere una precisione molto alta e calcolare la media esatta di una forma d’onda. In un segnale periodico, ed è il nostro caso perché si considera un solo ciclo, la tensione media Vmedia è uguale alla tensione RMS VRMS. Perciò la potenza media di un segnale sinusoidale periodico è data da Pmedia = (V_RMS^2)/R [W].
Possiamo adottare la formula per il nostro caso. Adesso si tratta di misurare la tensione di un ciclo a radiofrequenza e trovare il valore RMS. L’entità RMS non è applicabile alla potenza.
La moderna tecnologia ci fornisce uno strumento che fa al nostro caso. L’oscilloscopio digitale opportunamente collegato all’uscita del trasmettitore prima della linea di trasmissione con un probe a radiofrequenza adatto, è lo strumento che ci mette a disposizione tutti i dati per calcolare la potenza media.
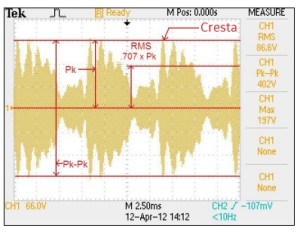
La figura 2 mostra la schermata di un segnale a radiofrequenza modulato, tipicamente SSB (Single Side Band).

L’oscilloscopio fornisce la tensione di cresta del ciclo di massima ampiezza, 197 V. Da questa tensione dobbiamo calcolare il valore RMS che vale 197 V* 0,707 = 139,3 VRMS. Non ci dobbiamo fidare del valore RMS di 86,6 VRMS trovato automaticamente dallo strumento perché è calcolato su tutti i cicli compresi nell’intervallo della base dei tempi, in questo caso 2,5ms. Se questo fosse un segnale a 14.250 kHz nello spazio di tempo citato, avremmo 35.625 cicli completi di cui l’oscilloscopio fa la media dei valori RMS.
Adesso abbiamo quasi tutti dati che ci servono. Ci manca la resistenza che conosciamo benissimo, è l’impedenza caratteristica della linea 50 Ω (ohm) considerandola adattata Z = R ± j0, puramente resistiva.
Applichiamo la formula adottata prima mettendo VRMS al quadrato: Pmedia = (V_RMS^2)/R sostituiamo 19.404/50Ω = 388 W (watt).
Ci chiediamo che tensione massima, nel ciclo di cresta, dobbiamo avere per non superare 500 W (watt)? Usiamo la formula inversa: VRMS = √((Pmedia*R) ) = √((500W*50Ω) ) = 158 VRMS. Moltiplichiamo la tensione RSM per 1,414 e troviamo la tensione massima di 223,4 V (volt) che dobbiamo leggere per non oltrepassare la potenza legale.
Per i segnali con portante continua di ampiezza costante, segnali periodici, quali CW (Continuos Waves/Radiotelegrafia Morse), FM (Frequency Modulation), nel tratto in assenza di modulazione, o RTTY (Radio Tele Type), le cose sono più semplici. La misurazione della tensione di cresta può essere fatta in qualsiasi punto della portante. Trovare, poi, la tensione RMS e applicare la formula della potenza media per trovare la potenza legale è cosa facile.
Ultima osservazione. Abbiamo parlato di tensione media di un ciclo di segnale sinusoidale che corrisponde al valore RMS nel caso di segnali periodici. Sappiamo, però, che la media di segnali sinusoidali è zero a meno che non utilizziamo il valore assoluto oppure che raddrizziamo una semionda. D’altra parte, non è questo che ci interessa ora. Abbiamo calcolato il valore RMS sul picco della tensione considerando un ciclo singolarmente. Ricordo, inoltre, che la potenza elettrica è sempre positiva, P = V*I, il prodotto algebrico nel semiciclo negativo della tensione e della corrente, in fase, con carico puramente resistivo, da risultato con segno positivo e frequenza doppia del segnale esaminato.
Fiorino/i3fdz
Biografia:
http://www.ab4oj.com/test/pwrmeas.html
http://www.acma.gov.au/theACMA/international-telecommunication-union
http://www.dudleylab.com/Appnote-4-Power-tests1.pdf Da cui sono state ricavate le due foto.
http://www.keysight.com/upload/cmc_upload/All/BTB_PowerBasics_2005.pdf?&cc=IT&lc=ita
http://www.boonton.com/~/media/Boonton/Webinars/RF%20Power%20Measurement%20Basics/RF_Power_Measurement_Basics.ashx